Il s'agit de disposer les entiers consécutifs, à partir de 1, sur les cases d'un quadrillage de manière à obtenir la même somme (appelée somme magique) sur les lignes, les colonnes et les diagonales
 Un
rapide essai permet de se rendre compte que la chose est impossible
Un
rapide essai permet de se rendre compte que la chose est impossible
avec un carré de 2 cases de côté.
La construction est en revanche possible avec un carré d'ordre 3. Commencez la recherche par la case centrale. Un seul des 9 chiffres peut y prendre place... (SOLUTION) Vous aurez ainsi vérifié que la somme magique du carré d'ordre 3 est 15. En effet, il n'y a qu'une seule somme magique possible par carré: le total des nombres divisé par la dimension, ce qui donne la formule :S = n(n+1)/2n = (n3+n)/2
Malgré la profusion de carrés magiques existants à partir de l'ordre 4, il est assez difficile d'en trouver un par tatonnement. Aussi différentes techniques ont-elles été recherchées. Malheureusement, aucune des méthodes trouvées à ce jour n'est applicable à tous les carrés magiques. De plus, les carrés d'ordre pair sont beaucoup plus difficiles à résoudre. Les plus anciennes méthodes connues datent du XVème siècle.
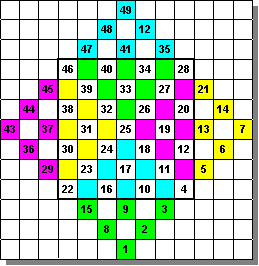
Bachet de Merignac (XVIIème siècle)est l'auteur d'une méthode applicable à tous les carrés d'ordre impair, assez simple d'emploi: Il suffit d'aligner les nombres sur les obliques d'un quadrillage puis de rabattre les 4 coins pour combler les cases restées vides. Ci-contre, un carré magique d'ordre 7 obtenu grace à cette méthode.
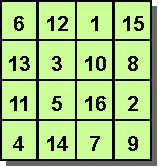
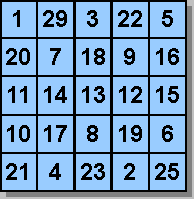
Saurez-vous trouver un carré magique d'ordre 4 ? (SOLUTION)
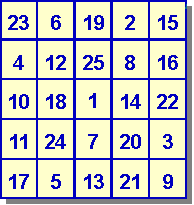
Le CARRÉ DIABOLIQUE (ou pan-magique) dans lequel la somme magique apparaît aussi sur les diagonales brisées. Saurez-vous en trouver un d'ordre 5 (le plus facile)? Utilisez pour cela la technique du cavalier inventée par Euler. Un cavalier placé au centre se déplace comme aux échecs pour écrire les nombres sur les cases où il passe. Quand il sort par un côté, il re-rentre par le côté opposé. Si la case d'arrivée est déjà prise, on descend sous la case de départ. (SOLUTION)
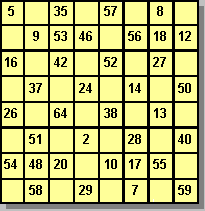
Le CARRÉ BI-MAGIQUE , très difficile à compléter, dont les lignes, colonnes et diagonales affichent la même somme pour les nombres mais également la même somme pour les carrés des nombres. On en trouve à partir de la dimension 8, comme celui ci-contre, que vous arriverez sans doute à terminer. (SOLUTION)
Le CARRÉ CABALISTIQUE est à la fois bi-magique et pan-magique.
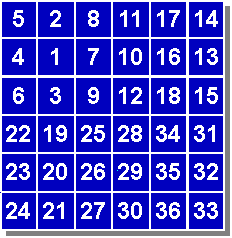
Le CARRÉ DE FRENICLE comporte des cases noires, en nombre égal sur les lignes et les colonnes. Saurez-vous compléter celui-ci, sachant que sa somme magique est égale à 42. (SOLUTION)
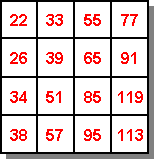
Dans le CARRÉ TRUQUÉ, deux cases se touchant par un coin contiennent des nombres premiers entre eux. Il devient alors impossible de respecter la suite des entiers naturels.
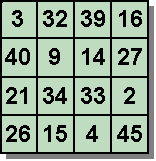
Le CARRÉ
SURTRUQUÉ est un carré truqué dont les
lignes colonnes et diagonales présentent la mème somme.
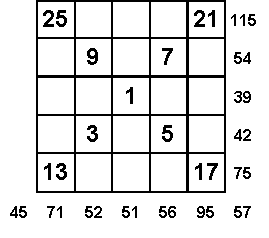
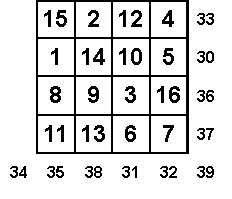
Un carré est
dit HÉTÉROGÈNE
lorsque les sommes de ses lignes, colonnes et diagonales sont toutes
différentes. (SOLUTION)
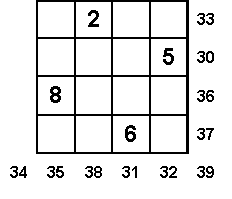
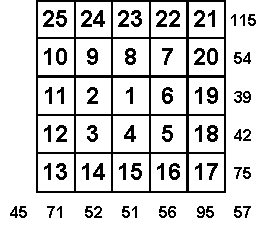
Dans un
CARRÉ ANTIMAGIQUE, les différentes sommes sont
consécutives. (SOLUTION)
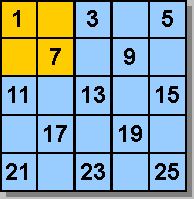
Dans un CARRÉ
ENCHANTÉ, chacun des quatre carrés élémentaires
de 4 cases affiche la même somme. (SOLUTION)

Au contraire, dans un CARRÉ
DÉSENCHANTÉ,
sur chaque carré élémentaire de 4 cases, les 4
différences des côtés ont une même somme.
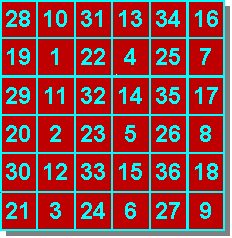
Dans le CARRÉ TALISMAN, les nombres de deux cases voisines diffèrent au moins d'un certain nombre. C'est le degrè du talisman. Celui reprèsentè ci-contre est de degrè 8
Citons encore le CARRÉ PRIMITIF dans lequel on remplace la suite des entiers naturels par celle des nombres premiers débarassée du nombre 2, génant parce que pair. Le plus petite dimension possible est 12 !
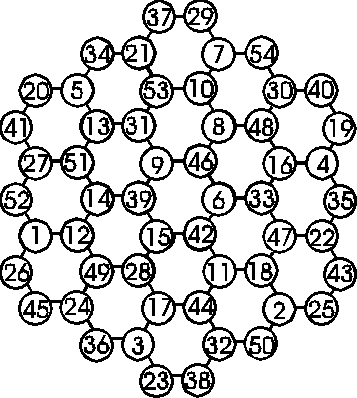
L'HEXAGONE MAGIQUE qui présente la même somme sur chaque alignement. (38) (SOLUTION)

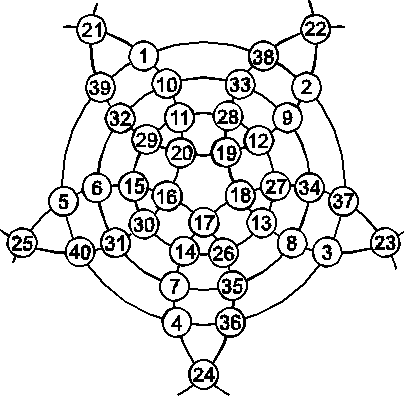
LES CERCLES MAGIQUES